Мероприятия

Математический калейдоскоп в регионах

Интерактивные площадки на основе проекта «Математические этюды»

Многогранники (6-9 классы) ссылка
Калейдоскоп и зеркальная симметрия (2-8 классы) ссылка
Геометрия для арифметики (5-9 классы) ссылка
Лабиринты (2-11 классы) ссылка
Вырезание из листа бумаги (2-11классы) ссылка
Гороховый конструктор (2-11 классы) ссылка

Многогранники

1. Для начала предлагаем посмотреть с детьми три этюда о внутренней геометрии многогранников:
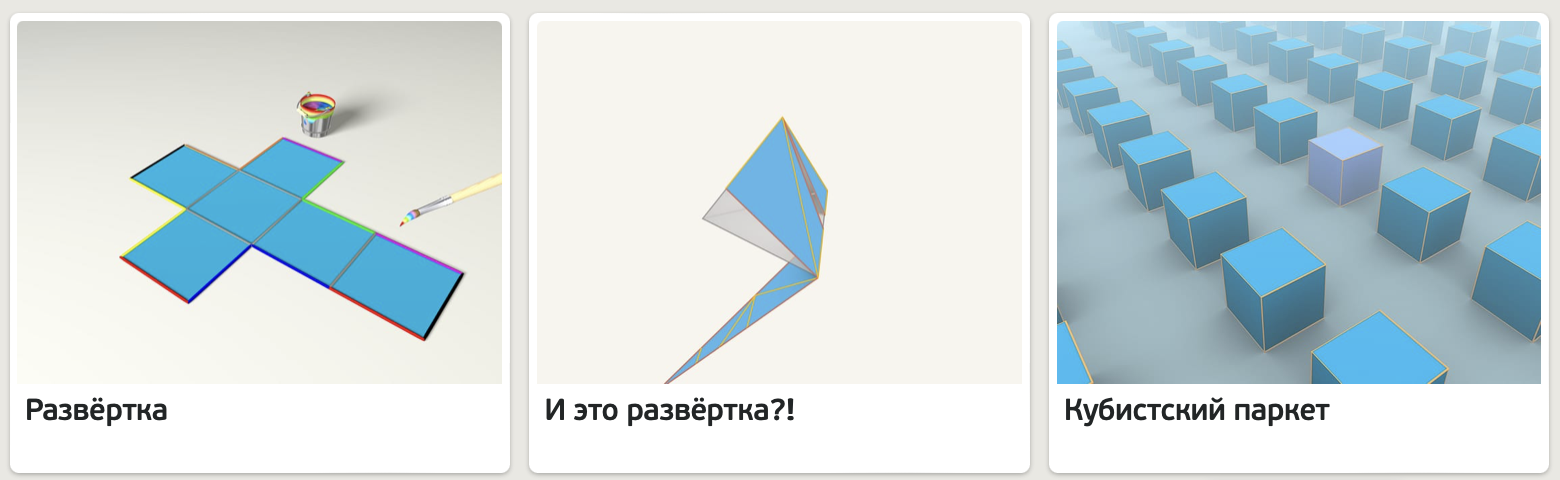
2. Разнообразие разверток куба.
Продемонстрируйте ребятам интерактивную модель разверток куба: https://www.geogebra.org/classic/davgtkzt
3. Упражнение. На каких из рисунков изображены развертки куба?
4. Практическая работа. Сборка многогранников из разверток.
Материалы для печати в формате PDF.
5. После сборки многогранников предлагаем обсудить с ребятами связь между тремя их характеристиками: числом рёбер, числом вершин и количеством граней.
На странице 27 выпуска 5 серии Библиотека «Математическое просвещение» размещено приложение о теореме Эйлера. Убедившись в её справедливости, предложите ребятам подумать над её доказательством.
https://etudes.ru/.data/localdocs/dolbilin.pdf

Калейдоскоп и зеркальная симметрия

Сложность: средняя.
Инвентарь: стопки листов А4, ножницы, несколько маркеров, несколько клеящих карандашей, пара зеркал, липкая лента.
Подготовка: закупка канцтоваров.
1. Для начала предлагаем посмотреть с детьми этюд.
2. Составление слов из симметричных букв. Загадки.
Перед входом в класс попросите ребят написать на листочке с липкой лентой в столбик печатными буквами своё имя. Затем приклеить его себе на грудь, а перед тем, как сесть за парту, посмотреться в зеркало и обратить внимание на свой бейдж. Обсудить, что необычного они заметили. Кто смог легко прочитать своё имя?
Что это такое? Попробуйте из этих половинчатых букв, прислоняя их к зеркалу, собрать слово. Можно разбить на команды, кто больше слов придумает. Записывать слова на доске.
Загадки
Вот гора, а у горы –
Две глубокие норы.
В этих норах воздух бродит:
То заходит, то выходит.
Ответ: Нос
Живет без тела,
говорит без языка,
никто его не видит,
а всякий слышит.
Ответ: Эхо
Ночь. Зима. На небе звезды.
Детки спят, совсем уж поздно,
Месяц на небе - рожок,
Выпал беленький ...
Ответ: Снежок
Что можно увидеть с закрытыми глазами?
Ответ: Сон
Простейшее лёгкое укрытие, представляет собой сооружение из жердей и палок, покрытых ветками, травой, защищает от ветра, зноя, холода и осадков.
Ответ: Шалаш
Дом - стеклянный пузырек,
И живет в нем огонек.
Днем он спит, А как проснется -
Ярким пламенем зажжется.
Ответ: Лампа
  • Что общего у всех этих загадок?
  • Все ответы к ним выглядят симметрично, если их записать вертикально.
  • Давайте разберемся, легко ли читать книгу, глядя в её отражение в зеркале?
  • Какие особенности есть у букв нашего алфавита?
  • Одни из них симметричные, другие - нет.
  • А что значит симметричные?
3. Определение видов осевой симметрии: горизонтальная, вертикальная и др.
  • Чем отличаются синие половинки букв от зелёных?
  • Какие из этих слов (тех, что на доске) составлены из синих?
Чтобы определить симметрию буквы, проведите мысленно ось через середину буквы. Сначала проведем горизонтальную ось.
Какие буквы имеют горизонтальную ось симметрии?
  • В, Е, Ж, 3, К, Н, О, С, Ф, X, Э Ю.
  • Теперь проведем вертикальную ось. Какие буквы, обладающие вертикальной симметрией, вы можете назвать?
  • А, Д, Ж, Л, М, Н, О, П, Т, Ф, Х, Ш.
  • А какие буквы могут быть и того, и другого цвета?
  • …
  • Какие геометрические фигуры могут быть отнесены к каждому из видов осевой симметрии?
  • Б, Г, Й, Р, Ц, Ч, У, Щ, Ъ, Ы, Ь, Я – не обладают симметрией.
  • А, Л, М, П, Т, Ш, Д – могут быть записаны так, чтобы возникала симметрия относительно вертикальной оси.
  • В, Е, К, С, З, Э, Ю - горизонтальная ось симметрии.
  • И, О – центральная симметрия.
  • Ж, О, Н, Х, Ф - две осевые симметрии.
4. Между двух зеркал, эксперимент с геометрическими фигурами
  • А что произойдет с объектом если мы его поместим между двумя зеркалами? Давайте понаблюдаем.
  • Проведите серию экспериментов с пирамидкой (или правильным треугольником на бумаге) и двумя зеркалами. Начиная со 180°, уменьшать угол до 0.
  • Что мы наблюдали?
  • Мы видели то два отражения, то три, то четыре и так далее. При определённых углах мы видим «красивое» изображение, то есть пирамидка помещается целиком, а при других появляются отдельные её куски (фрагменты).
  • Если разместить пирамидку между двумя параллельными зеркалами (угол 0), мы увидим бесконечный коридор и огромное количество пирамидок.
  • Где вы встречали подобные узоры из многократных отражений?
Калейдоскоп (в переводе с греческого означает "смотрю красивый вид") - это не только детская игрушка, в которой разноцветные кусочки стекла, многократно отражаясь в трех зеркалах, создают красивый узор. Зеркала эти расположены как боковые грани правильной треугольной призмы. Если бы эти углы были другими, то отражения могли бы накладываться друг на друга, и мы бы не увидели красивого симметричного узора.
  • Давайте соберём свой калейдоскоп и попробуем разобраться, как получается этот узор.
  • Для начала на бумаге попробуем отразить одну букву относительно двух зеркал. Например “Я” так, как это показано на листах задания.
  • Теперь попробуем с треугольником на том же листе для зеркал под углом 120 градусов.
5. Конструирование калейдоскопа
Настоящий калейдоскоп можно собрать, если
  • взять три зеркальные полоски, положить их зеркалом вниз на расстоянии 2 мм
  • попарно, вдоль всей длины соединить изолентой
  • перевернуть, сложить в форме крыши домика и склеить последние две полоски
  • сделать рисунок на листочке (примерно 7 см на 7 см)
  • прикрепить рисунок к одному из уголков калейдоскопа при помощи булавки (под изолентой) так, чтобы его можно было вращать и менять наблюдаемое изображение. Рисунок лучше сделать простым, например, геометрические фигуры, чтобы было проще наблюдать за его отражениями.
  • Калейдоскоп готов. Попробуйте определить, какое изображение настоящее. А как получаются соседние с ним треугольники?

Геометрия для арифметики

1. Познакомьтесь с
2. Проверьте понимание детьми изученного материала на серии упражнений:
  • Посчитайте в уме сумму натуральных чисел от 1 до 200.
  • Посчитайте в уме сумму нечётных чисел от 1 до 100.
  • Посчитайте в уме сумму квадратов чисел от 1 до 10.
  • Для учащихся старших классов возможно развитие темы.

Видеозаписи научно-популярных лекций по математике из медиатеки АГУ

Научно-популярные лекции для широкой аудитории (учащиеся, родители) могут выступать одним из элементов проведения мероприятия.
Лекции можно организовать в учебных аудиториях или актовых залах, оборудованных ЖК-экраном, интерактивной доской или проектором. По завершении лекции можно организовать ее обсуждение со слушателями.
Лекции записаны в рамках научно-популярного проекта «Наука вокруг» Адыгейского государственного университета.
1. https://naukavokrug.adygnet.ru/ — лекции и онлайн-уроки проекта «Наука вокруг»
Рекомендуемые лекции:
  • А.В. Савватеев «Математика погони на электросамокате»
продолжительность: 46:42
https://vk.com/video-226174019_456239054?ref_domain=naukavokrug.adygnet.ru
  • А.М. Райгородский «Математика интернета»
продолжительность: 53:03
https://vk.com/video/@naukavokrug01?z=video-226174019_456239025%2Fclub226174019
  • А.М. Райгородский «Красота математики в ее задачах»
продолжительность: 1:01:56
https://vk.com/video-226174019_456239025?ref_domain=naukavokrug.adygnet.ru
  • Н.Н. Андреев «Картография и кривизна»
продолжительность: 48:37
https://vk.com/video/@naukavokrug01?z=video-226174019_456239063%2Fclub226174019
  • Д.К. Мамий «Математика спортивных состязаний»
продолжительность: 53:42
https://vk.com/video/@naukavokrug01?z=video-226174019_456239034%2Fclub226174019
  • А.В. Савватеев «Математика в спорте, музыке, астрономии»
продолжительность: 45:48
https://vk.com/video-226174019_456239064?ref_domain=naukavokrug.adygnet.ru
  • А.В. Савватеев «7 величайших констант в математике»
продолжительность: 42:39
https://vk.com/video/@naukavokrug01?z=video-226174019_456239022%2Fclub226174019
2. https://etudes.ru/etudes/ — проект «Математические этюды»

Экскурсия по математическому парку

Музей математики под открытым небом в Майкопе — вписанная в городское пространство коллекция экспонатов, иллюстрирующих интересные математические факты.
Сайт проекта https://museum.adygmath.ru/ru/.

Приглашаем на виртуальную экскурсию в наш математический парк по ссылке https://vk.com/video-226174019_456239071
2024-12-01 09:00